2.2.2.3 Exact Hertz problem definition and its solution in a general form

Let two solids be in a point contact (Fig. 1). We have to adopt the following simplifying assumptions [1]:

Bodies are filled with uniform isotropic linearly elastic media characterized by Young's moduli , and Poisson ratios , .
The surfaces curvature weakly affects the mode of deformation.
Boundary surfaces are interchanged by the elliptic paraboloid.
The point of contact is not the singular point, the contact area is the simply connected domain and its contour is ellipse.

Fig. 1. Two bodies contact before deformation.

Fig. 2. Deformation two bodies. Surfaces before deformation are shown by dotted line, and squeezed surfaces – full line. The characters and denote lengths, which are determined by equations (1) and (2).

The equation of surface near the point of contact is as follows

(1)

where summation is conducted over doubly recurring indices , . The tensor characterizes the surface curvature and its principal values are and (here 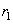, – principal radii of contacting surfaces in point O).

Similarly, for the second body:

(2)

Suppose the bodies are compressed by some force and as a result they become deformed and approach each other within small distance (Fig. 2). Then, the contact area will not be a point but surface portion having area ( for an ellipse). Let and be the components (along the and axes respectively) of displacement vectors of both bodies surface points at compression (Fig. 2).

From the picture it is seen that for the points of the contact area the following equation is valid:

(3)

(4)

For points outside the contact area the following is true:

(5)

Choose the axes 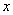and 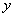directions so that tensor principal axes diagonalize it. Denoting by and the principal values of this tensor, rewrite it as (4):

(6)

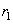Quantities and are related to curvature radii , and , of both surfaces by following formulas given here without derivation:

(7)

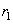where – angle between those normal sections of surfaces which have curvature radii and . Sings of curvature radii are considered to be positive if corresponding centers of curvature are located inside the corresponding body and negative in the opposite case.

Denote by the pressure between compressed bodies in a point of their contact. The pressure outside the contact area is evidently . Displacement under the action of normal forces is determined by the following expression (surfaces are considered to be plane):

(8)

Notice that from (8) it follows that ratio is constant and is equal to:

(9)

Relations (7) and (9) directly determine the deformations and distribution across the contact area. Substituting expressions (8) into (7) we get:

(10)

This integral equation describes pressure distribution across the contact area. Its solution can be found by computing technique used in the potential theory.

That is why we must consider the problem from the potential theory.

Let the charge with density be uniformly distributed over the triaxial ellipsoid

(11)

Then the potential inside the ellipsoid is determined by the following expression:

(12)

In the extreme case of almost plane (in the -direction) ellipsoid, i.e. when , the potential is:

(13)

(-coordinates inside the ellipsoid are supposed zero).

The expression for the potential can be written in the other way:

(14)

where integration is performed over the ellipsoid volume. Assuming , supposing in the radicand and integrating by within , we get:

(15)

where integration is performed over the ellipse area. Equating both expressions for , we get the following:

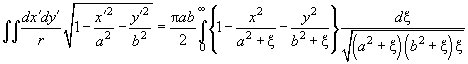
(16)

Compare the integral equation (16) and equation (10). It is seen that the right sides of equations contain similar quadratic functions of 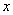and 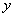while the left sides contain integrals of the same type. Therefore, it is clear that the contact zone (which is the region of integration in integral (10)) is limited by ellipse of the following type:

(17)

and that function should be as follows:

(18)

The const is chosen so that integral over the contact area is equal to force of bodies compression. The result is:

(19)

This formula determines the pressure distribution over the contact area. Notice that pressure at the center is half as much again the average pressure .

Substitute (19) into (10) and replace the resulting integral by its expression in accordance with (16):

(20)

where – effective Young's modulus:

(21)

Equating coefficients at and as well as absolute terms of both sides, we get:

(22)

(23)

(24)

Equations (22), (23) define semi-axes and of the contact area at given force ( and are known quantities for given bodies). Next, using expression (22), we can obtain the relationship between force and bodies penetration caused by it. Integrals in the right sides of equations are elliptical.

Applying the obtained formulas to the case of two spheres with radii and contact, we can write:

(25)

From the case symmetry it follows that , i.e. the contact area is circle which radius can be calculated from (23), (24) as:

(26)

in this case is the difference between the sum and the spheres center-to-center distance. From (18) the following relationship between and can be obtained:

(27)

So and correspondingly .

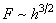Dependence of the , type is valid not only for spheres but for another bodies of finite dimensions. It can be easily proven from the similarity consideration. If we substitute , , , where – arbitrary constant, equations (23), (24) will not change. The right side of equation (22) will be multiplied by , therefore, it will be unchanged if is substituted for . From this it follows that should be proportional to .

Summary.

The Hertz problem allows to determine parameters of deformation in a "point" of two bodies contact.
Definition of the Hertz problem implies the use of uniform isotropic linearly elastic media model and the assumption of deformations smallness.
In a place of the tip-sample "point" contact the contact area arises.
The Hertz problem solution relates the deformation and applied load. Penetration is proportional to the compressing force as .

References.

Landau L.D., Livshits E.M. Theory of elasticity – Nauka, 1987. – 246 p. (in Russian)