2.2.7.5 Comparison of DMT, JKR and Maugis models
To compare the foregoing models we introduce the normalized radius of the contact area
, force
and penetration depth
:
,
,
(1)
In Table 1 are collected major assumptions and restrictions of every theory while in Table 2 – corresponding normalized equations [1].
| Model | Assumptions | Restrictions |
| Hertz | No surface forces | Not applied to small loads in the presence of surface forces |
| DMT | Long-range surface forces act only outside the contact area. Model geometry is as in the Hertz model | Contact area can be decreased due to the limited geometry. Applied only to small  |
| JKR | Short-range surface forces act only within the contact area | Force magnitude can be decreased due to surface forces.Applied only to large |
| Maugis | Tip-sample interface is modeled as a ring. | The solution is analytical but equations are parametric. Applied to all values. |
Table 1. Comparison of quantitative adhesion models.
| Model | Normalized equations |
| Hertz |   |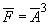
| DMT |   |
| JKR |   |
| Maugis |    |
Table 2. Normalized equations of quantitative adhesion models.
Fig. 1 shows plots of normalized force vs. normalized penetration depth for DMT, JKR and Maugis models at different
. As can be seen, at small
the Maugis model approaches the DMT model while at large
– the JKR model.
Fig. 1. Plot of the force vs. the penetration depth for the DMT, JKR and Maugis models
for the different
values.
Summary.
- Several theoretical models of adhesion having different ranges of application are proposed. The most accurate one is the Maugis model.
References.
- Handbook of Micro/Nanotribology / Ed. by Bhushan Bharat. - 2d ed. - Boca Raton etc.: CRC press, 1999. – 859 p.